確率とは何か。その問いは主観的確率と客観的確率の立場的違いから前世紀に長く統計学の哲学において論争の的となってきた問いである。今さらこの問いをのこのこと持ち出してきたのは、改めて確率論における立場の違いを蒸し返すようなことをしたかったわけではない。統計的機械学習に関わる研究者である以前に、単に現代に生きる一人の人間として、心のなかに素朴に抱いている違和感を記しておきたかっただけにすぎない。

相対頻度の世界

　今世紀は誰が改めて言うまでもなく、データの世紀である。人間行動に関わるあらゆるデータを蓄積し、そこから有益な法則性を導き出すための智慧と計算資源を持ち、得られた知見を社会実装に移すことができた人間が大きな力を掴んでいるということは論を俟たないだろう。データ科学の発展は著しく、私たち研究者はいかに従来よりも高級な性質を持ったツールボックスを作り出すかということに腐心しているわけだが、データ分析の根幹に胚胎している考え方は何の難しいことはない、「あるイベントはどれくらい起こりやすいか」を過去に蓄積した情報から推測することである。麻雀で一向聴のときに一牌と五牌のどちらかを切れと言われたら、（普通の局面では）役になりにくい一牌を切るのが普通だろう（断っておくが、私は麻雀は素人で嗜む程度なので、麻雀の戦略としてより妥当な方法を論じようとしているわけではない。麻雀については専門家諸氏に個人的にレクチャーしてもらえることを楽しみにしている）。過去の経験の蓄積からどちらの方が上がりやすいか実績がわかっていればそうするだろうし、場合の数の計算を多少行えばただちにわかる事実でもある。このとき、私たちは五牌を握っていたほうが和了れる「確率が高い」と言う。この「確率」は何を意味しているだろうか。私たちの念頭に自然と存在している前提は「次にツモる牌が一様ランダムである」ことであり、そのとき「すべてのあり得る局面の中で和了れる局面は何通りあるか」の相対頻度のことを称して「確率」と呼ぶのが少なくとも日常語としての「確率」の用語法と考えて差し支えないだろう。

　確率はより古くにはだいたい17世紀頃にまでその基本的な概念の発祥を遡ることができる。こう聞くと意外に最近に思われるかもしれないが、当時のアムステルダム市において生命保険の設計が市の財政上重要な課題となっており、そのために市民の平均寿命を見積もる必要に駆られていた。何十代であればどれくらいの割合で生きているか、という、まさに相対頻度による確率モデリングである。他にも同時期に教会裁判における証拠・証言の「確からしさ」を定量化するために「脱オカルト」化する過程で生まれたのが確率概念であったり、おそらくは確率概念の出自自体には絶対的なものはないと思われるが、相対頻度が一つのキーワードであると考えるのはそこまで的外れではないだろう。ちなみにこのあたりの確率の出自に関しては、イアン・ハッキング『確率の出現』に詳しい。

　相対頻度による確率概念の定式化は一見素朴ではあるが、意外に自明ではなく落とし穴が多く潜んでいる。まず、「相対」頻度は「理論」頻度とは異なることに注意されたい。公平なコインを100回投げて53回表が出たときの相対頻度は 0.53 であるが、私たちは「公平な」コインと呼ぶことによって表が出る理論頻度は 0.5 であることをアプリオリに措定している。数学的には、相対頻度と理論頻度を結びつける役者は大数の法則である。ここでは大数の弱法則を見る。

独立同分布に従う確率変数の無限列 $X_1, X_2, X_3, \dots$ が与えられたとき、その平均を $\mu$ とおく。標本平均 $\bar X_n=\frac1n\sum_{i=1}^nX_i$ と書くと、標本平均が理論平均 $\mu$ から大きく外れる確率は、十分大きい $n$ について限りなく小さくなる。すなわち $$\lim_{n\to\infty}\Pr\left[|\bar X_n-\mu|>\epsilon\right]=0$$ が任意の正数 $\epsilon$ について成立する。

平均 $\mu$ は理論頻度、標本平均 $\bar X_n$ は相対頻度と読み替えてよい。大数の弱法則が主張するのは、（適切な仮定のもとで）相対頻度は試行回数の十分大きい極限で理論頻度へと収束することである。しかし、「適切な仮定のもとで」の部分が想像以上に肝心であり、ここでは確率変数列の元はすべて $\mu$ を理論平均として持つことを要請している。私たちはあらかじめ措定した理論頻度に従ったコイン投げを行い、その結果として得られた観測系列から定まる相対頻度が理論頻度に回帰することを見ているのだ。

　例えば生命保険の例に戻ってみてほしい。仮にあなたの親戚に2型糖尿病患者がいる場合、遺伝的要因から通常は糖尿病リスクが高く見積もられる。このリスクの見積もりに確率論的・統計的分析が用いられていた場合、基本的にはあなたの「親戚に2型糖尿病患者がいる」という属性で階層化されたグループの糖尿病発生の理論頻度の存在がアプリオリに措定され、あなたの糖尿病発生のリスクが見積もられる。この分析モデルの意味論は、言い換えれば「『親戚に2型糖尿病患者がいる』人の糖尿病発生リスクは理論頻度 $\mu$ のコインに従っている」と措定していることに他ならない。生命保険の例でも同じだ。相対頻度に基づく平均寿命の算出モデルの意味論は、「あなたの年齢は X 歳だから余命は理論頻度 $\mu$ のコインに従っている」という世界観に帰着される。こうした世界観は合理的だろうか。注意してほしいのは、こうした世界観に「正しい」も「正しくない」も存在せず、在るのはどの世界観が私たちにとって「許容可能か」ということのみであるという点である。

　私が今年の7月に個人的に訪れたテュービンゲンの Bob Williamson は、こうした古典的確率論に異を唱えている。彼との議論で、主に三つの重要な観点があると思われた。第一に、理論頻度の存在をアプリオリに措定した確率論は乗り越えられる余地があることだ。先ほどの大数の法則の例で言えば、実際のところ、Cauchy 分布のように理論平均を持たない確率分布に従う確率変数列に対しては相対頻度の収束を保証することはできない。そうすると相対頻度に基づいたデータ分析はすべてが破綻してしまうのだろうか。そうではなく、理論を修正することで救い出す道は可能である。相対頻度の収束先が存在しなかったとしても、頻度はコンパクト集合上に値を持つから、従って集積点の集合は非空である。この相対頻度の集積点の集合を「確率」的なものとして再解釈できる余地があるだろう、と考えるのが、imprecise probability という概念である。概念としては意外に古く、George Boole や John Maynard Keynes など、多くの分野で横断的に発展してきた。詳しくは Fröhlich-Derr-Williamson'23 を参照。

　第二に、リスク選好性によってデータ分析における「理論頻度の措定」のバイアスを排除できる可能性があるという点である。最も有名な例は conditional value-at-risk (CVaR) である。ここではより一般的な形で示す。$X$ をリスク見積もりの対象となる確率変数とし、$w: [0,1]\to\mathbb{R}^+$ を非負の weight function とする。このとき、spectral risk measure と呼ばれるリスク尺度は $$R_w(X)=\int_0^1F_X^{-1}(q)w(q)\mathrm{d}q$$ で表される。ただし $F_X$ は $X$ の累積分布関数とする。Weight function を特に $$w(q)=\begin{cases}0&0 < q < \alpha \\ 1/(1-\alpha)&q \ge \alpha\end{cases}$$ と取れば CVaR となる。CVaR は確率変数 $X$ の値の上位 $\alpha$-分位点より上の確率の大きさをリスクとして見積もるため、「リスク回避型（risk-averse）」の尺度と呼ばれることがある。Spectral risk measure は CVaR の weight function $w$ に関する一般化として捉えるとわかりやすく、CVaR では上位 $\alpha$-分位点以上に一様な重みを置いていたのを、任意の分位点に好きなように重みを置くことができるようになった一般化である。これにより、ユーザーのリスクに対する選好を好きな weight function によって柔軟に表すことができる。この一般化によって、例えば誤差のモデル化を行うときに平均（つまり理論頻度）に拘泥することなく、ユーザーの意図に応じて柔軟にリスク尺度を設計することができるようになる。「自分は糖尿病発生リスクがそこまで高いとは思わないから、もう少しリスクに対して寛容なモデルを採用したい」といったことが可能になる。ちなみに数理的に面白いのは、なんとこの weight function は imprecise probability と凸共役の関係にある（！）ということだ。これに関しては Fröhlich-Williamson'24 の p19 を参照。

　第三に、データ・観測は「プロセス」に過ぎず、真実そのものではないということだ。昨今のデータ科学では、データには世界の「全て」が記述されており、とにかく大規模な計算資源を投下しさえすれば世界の法則を復元できるかといった勢いのある主張が見え隠れすることも少なくない。実際、深層学習、大規模言語モデル時代を通じて私たちコンピュータ科学者たちが学んできたことは、小手先の智慧なんかより計算機のスケールの方がずっと威力のあるものだった、という「苦い教訓」であるというのは見当違いではない。しかしそれが全てでもない。世界の状態を「（文字通り）全て」記述しつくすというのはいかに計算資源が豊富にあったとしてもそれが有限である以上は不可能だから、データとして残した時点でそれは不可避的に世界の状態の真部分集合になることを免れ得ない。そのデータを用いて復元した世界の状態は絶対に私たちの何らかの事前知識を入れた推測結果に過ぎないから、元の世界の状態と一致しているという確かな保証はどこにもないのだ。いわゆる帰納推論の不可能性のことを別の言葉で言っている。

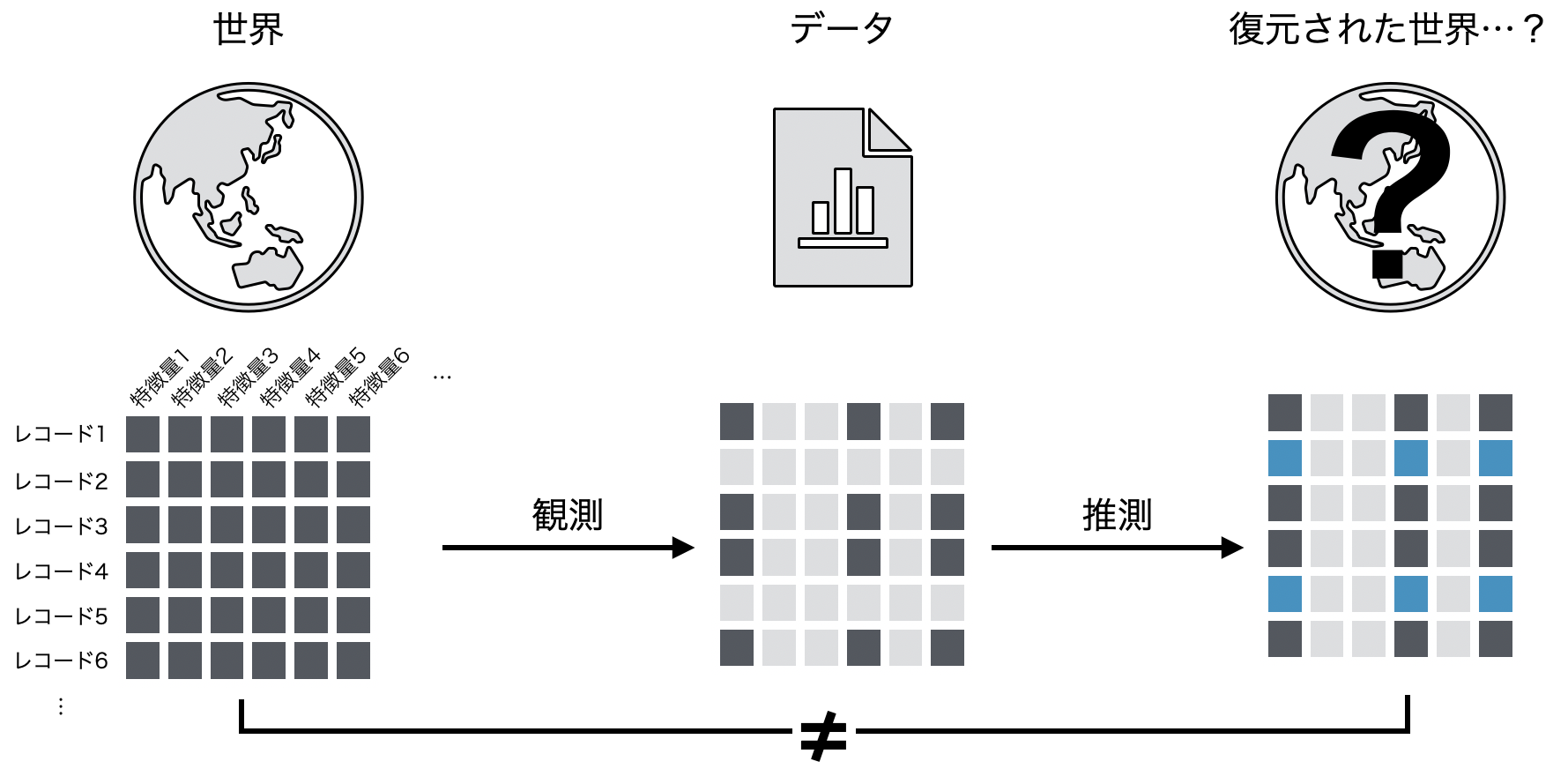
したがって、データは世界の状態を写し取る過程に過ぎず、絶対的な真理がそこに内在しているわけではなく、観測者の恣意すら混入する。どの特徴量を観測するべきかという選択自体が観測者の恣意である。恣意的な過程に過ぎないのだから、検証データに対してどれだけ高いベンチマーク予測性能が達成できたということには本質的に意味はない。それは「真の世界の状態」について語っているのではないから。私たちが考えなければならないのは、むしろデータをもとにして「どのような意思決定を下すのか」という点にある。データ、観測系列、ないし相対頻度は真実ではない。だから確率概念やリスク尺度をどのように定量化すべきかを常に考え続けなければならないのである。この第三の見方は Williamson'20 によく表現されている。

　平均に基づくデータ分析というのは一見非常にもっともらしい。しかし平均は仮構である。相対頻度の収束先として存在するのかどうか確かではない。私たちの一つ一つの意思決定がコイン投げに従っているとは思いづらい。いや、思いたくない、と言う方が正確か。データから全ての客観的法則と真実を知ることができると信奉することは畢竟、理論平均という仮構の奴隷に成り下がることなのかもしれない。確率やリスク尺度を考え直すことは真実を考え直すことではない。それは私たちがどのような意思決定をしたいと心のなかで思っているのかを明示化する過程である。

節約律の世界

　確率概念を考え直す試みは私が考えるまでもなく、歴史を紐解けばいくらでもある。しかも、機械学習の黎明期にそのアイデアの一つが眠っている。それがアルゴリズム情報理論（algorithmic information theory）と呼ばれる分野である。その創始者はダートマス会議の参加者でもある Ray Solomonoff であり、Solomonoff は アルゴリズム的確率（algorithmic probability） と呼ばれる、従来の相対頻度に基づく確率とは異なる確率概念を提唱している。ここではインフォーマルにその概念を紹介する。

$U$ を普遍 Turing 機械とし、プログラム $p$ を受け取って文字列 $x=U(p)\in\{0,1\}^*$を返すものとする。このとき、文字列 $x\in\{0,1\}^*$ のアルゴリズム的確率は $$M(x)=\sum_{p:U(p)=x*}2^{-\ell(p)}$$ で与えられる。ただし、$x*$ は文字列 $x$ から始まる任意の文字列とし、$\ell(p)$ はプログラム $p$ をビット列で表したときのプログラム長とする。

自然言語で言い換えると、ある文字列 $x$ の「確率」を定めるとき、まず世の中のあらゆる可能なプログラムを考え、その中で $x$ を出力の冒頭に持つようなプログラムのみを列挙し、そのようなプログラムの長さが短いほど高い確率を $x$ に付与することでアルゴリズム的確率は定義される。短いプログラムで出力しやすいほど現れやすい文字列であるというわけである。二点注意を挙げる。一つは、アルゴリズム的確率は必ずしも一般的な確率測度の公理を満たさない。特に規格化条件は満たされない。これは普遍 Turing 機械が任意のプログラムに対して必ずしも停止するとは限らないためである。そのため、$M(x)$ は semi-measure と呼ばれる類の測度になる。二つ目に、$M(x)$ の計算を実際に行うためにはすべての可能なプログラムを総列挙する必要があるため、厳密計算は不可能である。この点に関しては、DeepMind のグループが近似的にアルゴリズム的確率に基づいたメタ学習機械の提案を行っていたりする（Grau-Moya et al., 2024）。また、全く深くは触れないが、アルゴリズム的確率の概念は当然ながら Kolmogorov 複雑性の概念に密接に関連している。

　さて、アルゴリズム的確率の概念について少し考察してみたい。アルゴリズム的確率の面白い点の一つに、私たちが慣れ親しんでいる相対頻度の概念が一切定義に登場しない点があると思う。これの何が面白いか。頻度を用いなくても「確率」が定義できるということは、そもそも標本がなくても「確率」が定義できるということである。この事実からはまず実用的なご利益が得られる。例えば Theis'24 では画像の自然画像らしさを仮説検定するためのひとつのアイデアとして、検定対象の画像のアルゴリズム的確率を計算しさえすれば、自然画像集合との Kullback-Leibler 距離（KL 距離）を検定統計量として仮説検定可能なのではないかといった萌芽的アイデアを示している。このアイデアは従来の二標本検定に根ざしており、その場合は二つの標本間から経験 KL 距離を計算することになるわけだが、片方の標本が一点に縮退してしまうと KL 距離は計算できない。それをアルゴリズム的確率に置き換えてしまうことで（少なくとも操作的には）計算可能にできている点で興味深い。この手続きの意味論は現時点では何も確かなことはわかっていないが、仮説検定の枠組みの先へ進むうえで間違いなく面白い考え方の一つであると思う。

　そこで気になってくるのがアルゴリズム的確率の意味論である。相対頻度による確率値の特徴づけはコイン投げをイメージすればそれなりに直感的に意味論を理解できた（もちろん無限回のコイン投げの意味論など細かな点では自明ではない点はたくさんあるにはせよ）。再びアルゴリズム的確率 $M(x)$ の定義を振り返ると、$M(x)$ が大きな値を取るのはどのようなときかというと、文字列 $x$ がある非常に短いプログラム $p$ によって生成される場合である。これを言い換えれば、「より確からしいデータ $x$ はより短いプログラムで出力できるものである」ことを表明している。アルゴリズム的確率は相対頻度による特徴づけを排した代わりに、Occam の剃刀を指導原理とした確率論であるとも言える。しかしこの意味論には少なくない違和感を覚える。イベントの起こりやすさというある種の世界のモデル化に、「起こりやすい現象はすべて簡易に記述可能である」という（検証不能な）強い帰納バイアスが入っているからである。元々 Occam の剃刀は、「ある現象を同程度に確からしく説明可能な複数の仮説があったとき、最も冗長性の少ない仮説を選ぶのが説明として合理的である」ということを表明しているにすぎず、「最も冗長性の少ない仮説が真である」ことを主張する性質は持たない。Occam の剃刀を用いて「正しい」仮説を選ぼうとするのはよくある誤謬であり、現代医学でも例えば Whyte'18 によって以下のような箴言が提出されている。

It (=Occam’s razor) should be invoked only when several hypotheses explain the same set of facts equally well.

逆に言えば、短いからといって「正しい」仮説であるとは決して限らない。医学の例で言うと、要因数を絞った簡潔な診断が「正しい」疾病のメカニズムを捉えているとは限らない。それはあくまで一つの説明にすぎない。にもかかわらず、アルゴリズム的確率は記述長が短く節約的なデータがより確からしいことを標榜している点が、あたかも節約律を世界の法則として定立しているように見えるのである。前節の議論と歩調を合わせるのであれば、もちろんこうして定義されたアルゴリズム的確率を真理記述装置として用いることをせず、あくまで私たちの意思決定の糧として用いるに留めるのであればそれは何らかの理にかなっていると言えるわけだが、私たちが行おうとしている意思決定の内容に対して無思考的にアルゴリズム的確率を用いてしまうと、理論平均の呪縛から逃れたとしても今度は節約律の呪縛に囚われてしまうように思われるのだ。

　Occam の剃刀、節約律は何を前提として、いつ正当化され得るのだろうか。すぐに思いつくのは統計におけるモデル選択である。赤池情報量規準（AIC）、Mallow’s Cp、最小記述長原理（MDL）、バイアス・バリアンス分解。いずれも統計モデルが簡潔であることをよしとするモデル選択の指針である。ここでは Ryan Tibshirani のレクチャーノート に従って、モデル選択基準のひとつである degree of freedom と Efron の共分散公式、Stein の公式について確認し、節約律と統計モデルの選択について手短に直感を涵養する。ここでは1次元の最小二乗回帰を考え、観測は $\{(x_i,y_i)\}_{i=1}^n$、学習した回帰モデルは $\hat f$ とし、その汎化誤差を評価する。ちなみに数理統計では汎化誤差のことをよく “optimism” と呼ぶらしいので、ここでもその用語を踏襲する。 $$ \begin{aligned} \text{Opt}(\hat f) &= \underbrace{\mathbb{E}[(Y-\hat f(X))^2]}_{\text{予測誤差}} - \mathbb{E}\bigg[\underbrace{\frac1n\sum_{i=1}^n(Y_i-\hat f(X_i))^2}_{\text{訓練誤差}} \mid X\bigg] \\ &= \frac1n\sum_{i=1}^n\mathbb{E}\left[ (Y-\hat f(X_i))^2 - (Y_i-\hat f(X_i))^2 \mid X \right] \\ &= \frac2n\sum_{i=1}^n\mathbb{E}\left[ (Y_i-Y)\hat f(X_i) \mid X\right] \\ &= \frac2n\sum_{i=1}^n\text{Cov}[Y_i,\hat f(X_i)\mid X] \end{aligned} $$ ここでは回帰モデルとして誤差がゼロ平均であるような対称分布を想定している。このとき、optimism は実質 $Y$ と $\hat f(X)$ の共分散となる。これが Efron の共分散公式である。モデル選択の際に予測誤差を最小化するためには、訓練誤差を最小にしつつ、optimism を最小化する必要がある。そのため、モデルの degree of freedom を次のように定義する。 $$ \text{df}(\hat f) = \frac{1}{\sigma^2}\sum_{i=1}^n\text{Cov}[Y_i,\hat f(X_i)\mid X] $$ ここで $\sigma^2$ は誤差分布の分散とする。この degree of freedom は表式からのみでもそれなりの解釈ができる。Degree of freedom が大きいということは、モデル $\hat f$ は X-Y の関係を大きく「ばらつかせる」ことができる（ほどに表現力が高い）。さらに、Stein の公式を用いると degree of freedom は次のように表される。 $$ \text{df}(\hat f) = \mathbb{E}\left[\sum_{i=1}^n\frac{\partial\hat f(X_i)}{\partial Y_i} \mid X \right] $$ つまり、degree of freedom が大きいということはモデル $\hat f$ が出力に対して感度が大きいということになる。$\hat f$ が線形回帰モデルであれば、$\text{df}\propto p$（次元数）になることが簡単に確認できる。これは AIC でも見られる結果である。

　一度結論を確認する。回帰予測の場合、モデルの degree of freedom が小さいほうが柔軟性・出力のばらつきが小さく、そのとき訓練誤差が予測誤差からばらつきにくくなり汎化しやすくなる。この観点から節約律は正当化される。もう一歩踏み込めば、途中の「汎化しやすくなるから」のところを端折ってもよい。すると、「モデルの感度が低くなることを合理的と見なすなら、節約律は正当化される」と言い直すことができる。このとき、逆に言えば degree of freedom が小さいと訓練事例からかけ離れたような予測をしづらくなることになる。当たり前のことを言っているように見えるが、この事実は転移学習など訓練事例と予測事例の従う法則に乖離が存在するケースでは明らかに問題となる。

　閑話休題だが、節約律の別表現として、（動物）心理学における「モーガンの公準」も有名な例のひとつである。その主張内容は、「被験者の行動をより低次の心理過程で説明できるのであれば、高次の心理過程を要する説明を行うべきでない」ということになる。Clever Hans に対する反駁が有名であり、馬 Hans が計算をしているように見えたのは、別に Hans が本当に計算を行っていたのではなく、調教師の微妙な動きを読み取っていたからだった、というところに、高次の心理過程をできるだけ想定せずに説明すべきであるという原則が当てはまる。気になって動物行動の研究を行っている知人に「モーガンの公準は何を前提として正当化されるだろうか」と問うてみたところ、「獲得するための進化のコストが高い心理プロセスを想定するのは進化論的に妥当でないだろう」というアイデアが暗々裏にあるとのことであった。これも言い換えれば過去事例から将来事例へのある程度の「連続性」を措定したいという前提と言えるのではないだろうか。